When I was an undergraduate, computers were just beginning to be introduced into the university curriculum. Physics majors were expected to take a single semester of Pascal taught by the computer science department. We wrote programs to sort lists, process a payroll, and so forth, but were expected to acquire the specialized tools of scientific computing on our own. Most of us wasted many human and computer hours learning them by trial and error.

In recent years, many departments have added a computational physics course, taught by physicists, to their curricula. However, there is still considerable debate as to how this course should be organized. My philosophy is to use the upper division/graduate mathematical physics course as a model. Consider the following parallels between this text and a typical math physics book: A variety of numerical and analytical techniques used in physics are covered. Topics include ordinary and partial differential equations, linear algebra, Fourier transforms, integration, and probability. Because the text is written for physicists, these techniques are applied to solving realistic problems, many of which the students have encountered in other courses.

Numerical Methods for Physics is organized to cover what I believe are the most important, basic computational methods for physicists. The structure of the book differs considerably from the generic numerical analysis text. For example, about a third of the book is devoted to partial differential equations. This emphasis is natural considering the fundamental importance of Maxwell's equations, the Schrodinger equation, the Boltzmann equation, and so forth. Chapters 6 and 7 introduce some methods in computational fluid dynamics, an increasingly important topic in the fields of nonlinear physics, environmental physics, and astrophysics.

Numerical techniques may be classified as basic, advanced, and cutting edge. On the whole, this text covers only fundamental techniques; to work effectively with advanced numerical methods requires that the user first understand the basic algorithms. The discussion in the "Beyond This Chapter" section at the end of each chapter guides the reader to advanced algorithms and indicates when it is appropriate to use them. Unfortunately, the cutting edge moves so quickly that any attempt to summarize the latest algorithms would quickly be out of date.

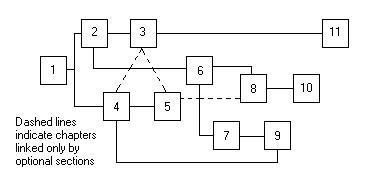
The material in this text may be arranged in various ways to suit anything from a 10-week, upper-division class to a full-semester, graduate course. Most chapters include optional sections that may be omitted without loss of continuity. Furthermore, entire chapters may be skipped; chapter interdependencies are indicated in the flow chart.

I have tried to present the algorithms in a clear, universal form that would allow the reader to easily implement them in any language. The programs are given in outline form in the main text with MATLAB and C++ listings in the appendices. In my classes, the students are allowed to use any language, yet I find that most end up using MATLAB. Its plotting utilities are particularly good---all the graphical results in the book were generated directly from the MATLAB programs. Advanced programmers (and students wishing to improve this skill) prefer using C++. FORTRAN versions of the programs, along with the MATLAB and C++ source code, are available online from Prentice Hall.

The over 250 exercises should be regarded as an essential part of the text. The time needed to do a problem ranges from 30 minutes to 2 days; in my classes, I assign about five exercises per week. Each exercise is labeled as:

[Pencil]	can be solved with pencil and paper.
[Computer]	requires using the computer.
[MATLAB]	best solved using MATLAB.
[C++]	best solved using C++.

While some texts emphasize month-long projects, I find that shorter exercises allow the class to move at a brisker pace, covering a wider variety of topics. Some instructors may wish to give one or two longer assignments, and many of the exercises may be expanded into such projects.

Readers familiar with the first edition will notice the following changes: C++ versions of the programs have been added, along with a new section (1.3) summarizing the language. The MATLAB programs have been updated to version 5. The discussion of derivatives has been moved from Chapter 1 to Chapter 2. A new section (6.3) has been added to Chapter 6. The discussion of hyperbolic partial differential equations has been collected into a new Chapter 7.

I wish to thank the people in my department, especially D. Strandburg, P. Hamill, A. Tucker, and J. Becker, for their strong support; my students and teaching assistants, J. Stroh, S. Moon, and D. Olson, who braved the rough waters of the early drafts; the National Science Foundation for its support of the computational physics program at San Jose State University; my editors at Prentice Hall and the technical staff of The MathWorks Inc. for their assistance; the National Oceanic and Atmospheric Administration Climate Monitoring and Diagnostics Laboratory for the CO data used in Chapter 5. In addition, I appreciate the comments of the following reviewers: David A. Boness, Seattle University; Wolfgang Christian, Davidson College; David M. Cook, Lawrence University; Harvey Gould, Clark University; Cleve Moler, The MathWorks, Inc; Cecile Penland, University of Colorado, Boulder; and Ross L. Spencer, Brigham Young University. Finally, I owe a special debt of gratitude to my entire family for their moral support as I wrote this book.